Il Numero e le Sue Rappresentazioni - Il Numero Cardinale

Dalla Corrispondenza Biunivoca alla Costruzione di Insiemi Modello

Scrive Bertrand Russell: "Debbono esserci voluti secoli e secoli per scoprire che una coppia di fagiani e un paio di giorni sono entrambi esemplari del numero 2".
Il passaggio successivo alla corrispondenza biunivoca, cui si riferisce Russell, è infatti quello di creare insiemi modello che possano essere messi in corrispondenza biunivoca con l'insieme dato.
Poiché il numero è un'astrazione, di fatto il confronto si realizza tra un gruppo di oggetti e un modello di cui conosciamo la potenza.

I numeri in colore sono composti da regoli di colore e grandezza diversa. Il regolo bianco rappresenta il numero uno. Gli altri regoli seguono la regola: uno di più.

Proponiamo alcune attività:

1. Prepariamo alcune scatole sulle quali applicheremo un certo numero di contrassegni sotto forma di bolli adesivi ( da 1 a 9) e chiediamo agli alunni di inserire in bustine trasparenti alcuni gettoni o biglie colorate ( non più di nove) e di metterle nella scatola che ha la stessa "potenza".
2. Su ogni scatola applicheremo l'etichetta di un contatore che nella fase iniziale può essere costituito da uno dei numeri in colore. Facciamo cercare ai bambini stessi quali contrassegni utilizzare come rappresentazione di un certo modello lasciandoli liberi di utilizzare i simboli che essi stessi hanno scelto purché venga indicata la giusta numerosità del modello.
3. Chiediamo ai bambini di cercare gruppi di oggetti equipotenti a quelli indicati sulla scatola esempio una certa quantità di libri (tre) sono tanti quanti le biglie di una certa scatola. Possiamo a questo punto indicare la quantità del gruppo considerato con i contatori.
4. Chiediamo agli alunni di stabilire l'equipotenza tra un gruppo di oggetti e quelli di una serie appositamente preparata.
5. Chiediamo agli alunni di portare (o disegnare) la quantità corrispondente ad un contatore.

Sorgerà a questo punto il bisogno di un accordo ricorrendo alla simbologia universale. Si useranno quindi gli stessi segni, le stesse cifre che i bambini stessi vedono sul calendario, nelle vetrine dei negozi. I numeri arabi, e le parole che li indicano andranno così a sostituire i segni da loro scelti.

I Numeri in Colore

Colora i regoli.

Colora con i colori dei regoli e scrivi il numero corrispondente.

Completa il muro del 5:

Comporre e Scomporre

Il Domino dei Numeri

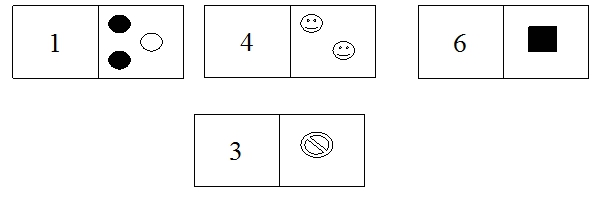
• Prepariamo 36 tessere di cartoncino di forma rettangolare, dividiamole a metà con una riga nera, scriviamo su una parte un numero da 1 a 9 e sull'altra parte disegniamo collezioni di oggetti che vadano da 1 a 9, badando a non associare il numero alla quantità corrispondente.
• Ecco un esempio di tessere.

  

Il numero dei giocatori può variare badando che ciascun giocatore abbia lo stesso numero di tessere. Dopo averle distribuite il primo giocatore tira giù una tessera. Se il giocatore successivo ha una tessera nella quale è rappresentata la quantità corrispondente al numero o il numero corrispondente alla quantità della tessera che sta sul tavolo, la tira giù e la dispone al posto giusto ad una delle due estremità altrimenti passa la mano al vicino.

Vince chi per primo resta senza tessere.

I Numeri... nei Sacchetti

L'acquisizione del concetto di numero cardinale non si limita ovviamente alla capacità di leggere e scrivere i numeri. Per consolidarne il concetto è necessario che il bambino entri nei meccanismi di composizione e scomposizione attraverso giochi, attività, che prevedano la manipolazione la rappresentazione grafica per passare quindi al linguaggio dei numeri con l'uso dei segni di addizione e sottrazione.
Saper comporre i numeri naturali implica un notevole passo avanti nel processo di astrazione in quanto si passa dalla manipolazione di quantità concrete ai simboli numerici.

• Data una coppia di sacchetti cominciamo dal numero zero e cerchiamo tutte le combinazioni per formare quantità di elementi (i cubetti dei numeri incolore) da 0 a 10.
• Nel caso dello 0, come è evidente, c'è solo una possibilità: due sacchetti entrambi vuoti, sia il primo che il secondo.
• Se si ha un solo cubetto, le possibilità sono 2.
• Procedi prendendo di volta in volta 2 – 3 – 4 - 5 cubetti.
• Ogni possibilità indicata richiama la combinazione inversa, i cubetti possono infatti essere disposti sia nel primo che nel secondo sacchetto.

La Rappresentazione

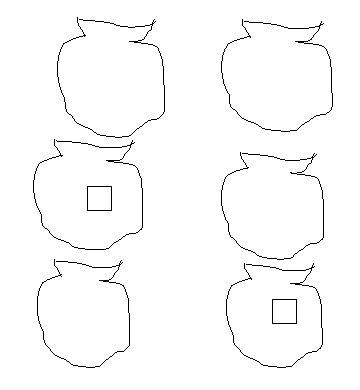
• Una volta operate concretamente con le coppie di sacchetti queste operazioni vanno rappresentate graficamente, su un cartellone e sul quaderno come nell'esempio seguente.

  

• Al centro viene disegnata la quantità di elementi di cui si vogliono trovare combinazioni per la composizione, attorno si rappresentano le combinazioni possibili.

Fa che Siano...

L'attività che proponiamo ci permette di andare oltre la scomposizione del numero in quanto consente ai nostri alunni di esercitarsi nel calcolo orale offrendo loro la possibilità di verificare l'esattezza delle risposte.

• Mettiamo dentro un bicchierino di plastica ad esempio, 3 palline. Chiediamo ad un bambino di farli diventare... 8 mettendo in uno o più bicchierini le biglie che mancano secondo il criterio che riterrà più opportuno.
• Facciamo vuotare da un altro bambino il contenuto di tutti i bicchierini in un piatto per verificare se la soluzione proposta è giusta. Nel caso in cui le biglie non risultino essere... 8 facciamo provare un altro bambino, finché non avremo verificato che la soluzione ipotizzata sia quella giusta.
• Facciamo registrare la situazione corretta nel modo seguente:

  

Variante: Togliere invece che Mettere

Proponiamo ora una attività analoga in cui però si chiede di "togliere".

• Mettiamo sul piatto 15 biglie, facciamole contare e chiediamo ai bambini: "Fai in modo che siano 7".
• Anche in questo caso è possibile utilizzare più di un bicchierino per arrivare al numero di biglie richieste. È possibile quindi che si verifichi la seguente situazione:

  

• Dividiamo i nostri alunni in piccoli gruppi, distribuiamo ad ogni gruppo biglie, piatti e bicchieri di plastica a sufficienza e chiediamo loro di inventare almeno 3 situazioni in cui bisogna fare in modo che diventino 9.
• Chiediamo a ciascun gruppo di registrare sul quadernone le situazioni individuate.
• Raccogliamo i risultati su un cartellone.

Le Freccette

Costruiamo un tirassegno per freccette disegnando su un cartoncino bianco 5 centri concentrici, ed assegniamo a ciascun cerchio un punteggio. Chiamiamo due giocatori e decidiamo il numero di lanci per ogni giocatore.

Procuriamoci delle freccette bianche e nere e facciamo giocare due bambini per volta.
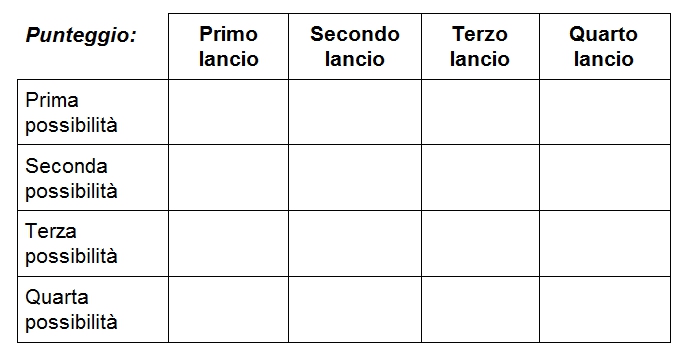
Registriamo il punteggio su una tabella come la seguente:

• Dopo aver fatto effettuare alcune partite chiediamo ai nostri alunni di scoprire qual è il punteggio massimo e il punteggio minimo. Facciamo osservare loro che entrambi i punteggi si possono raggiungere in un solo modo, ovvero ottenendo per quattro volte lo stesso punteggio.
• Facciamo definire gli altri possibili punteggi e facciamoli registrare su una tabella.